Blog PostAboutGithub

Dijkstra's Algorithm

Purpose: Dijkstra's algorithm is used to find the shortest paths between a source vertex and all other vertices in a graph with nonnegative weights. Djikstra's can also solve the more specific problem of finding the shortest path from a start vertex to an end vertex. One use case could be finding directions from Point A to Point B using roads on a map.

Runtime: O((E+V)logV) for a simple python implementation (see below), where E is the number of edges and V is the number of vertices.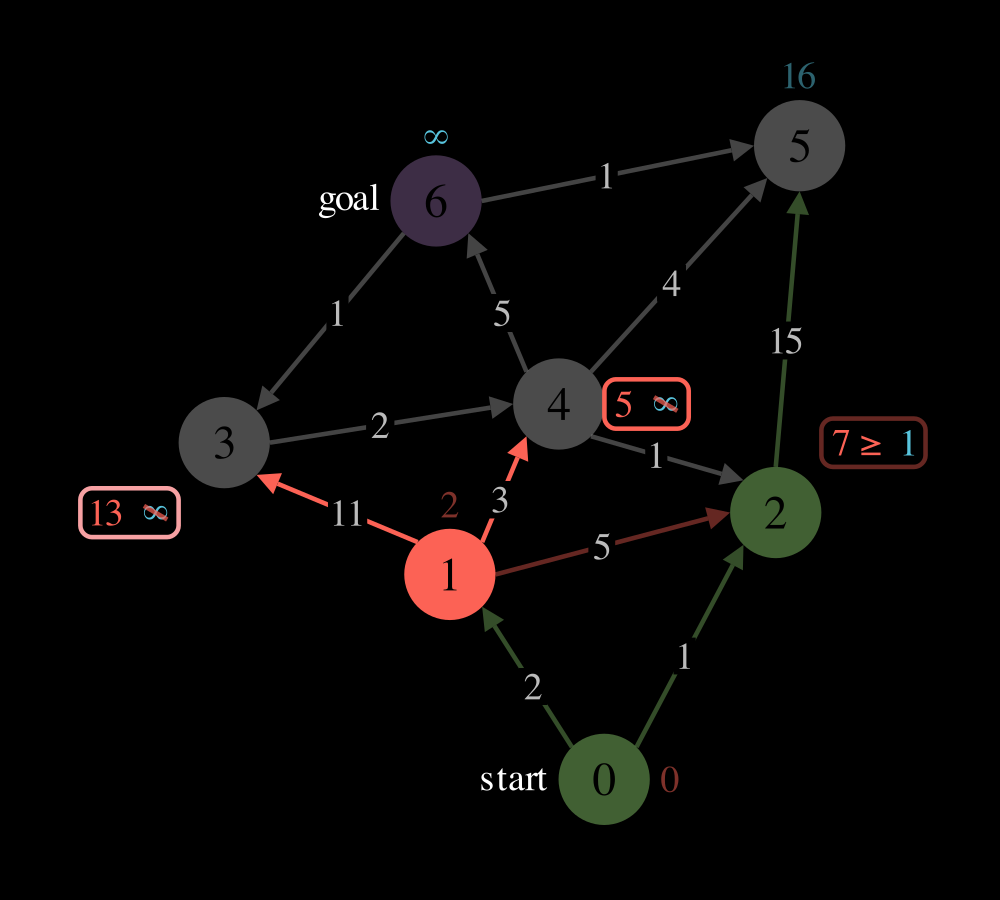

Algorithm Steps:
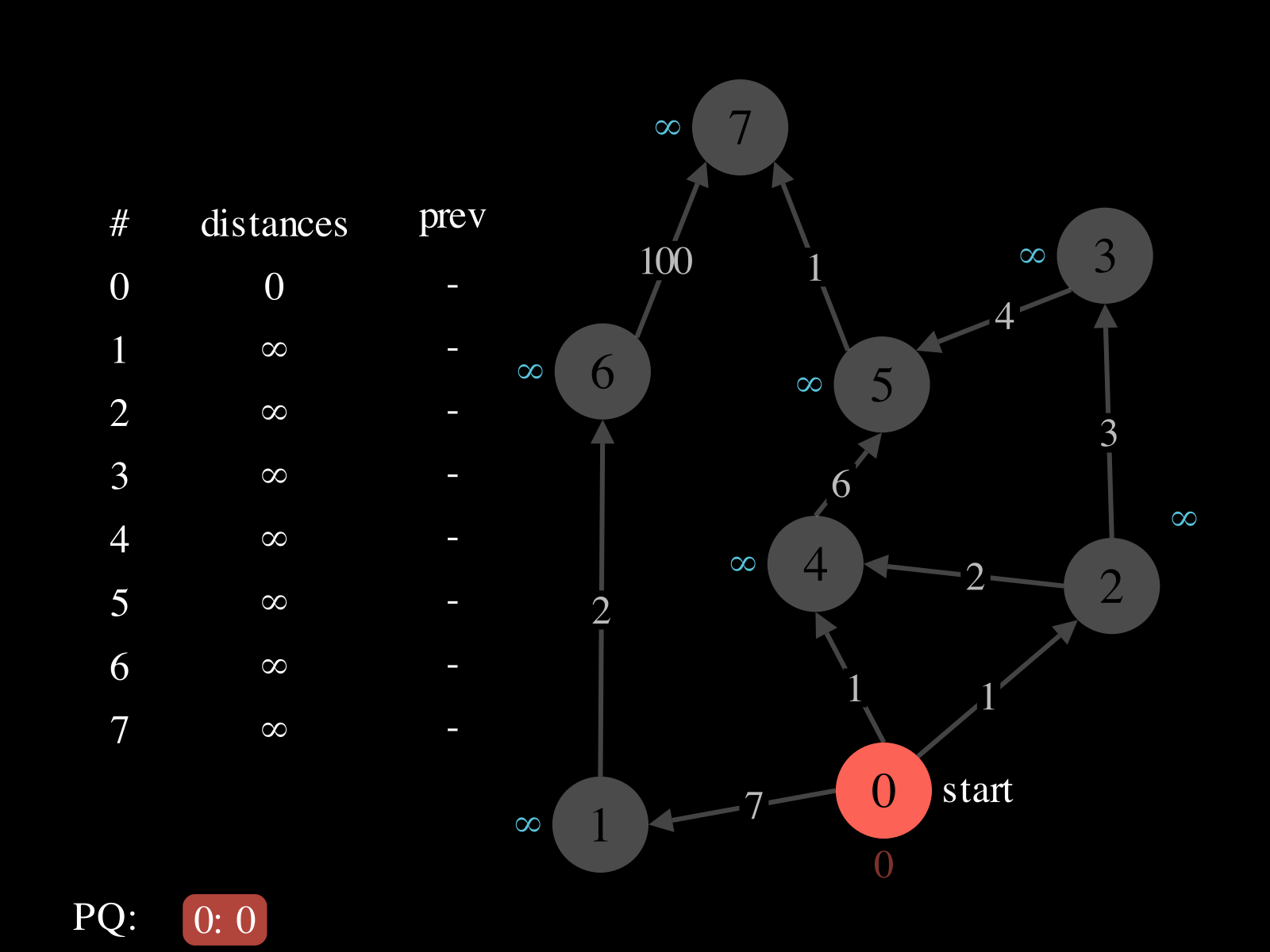
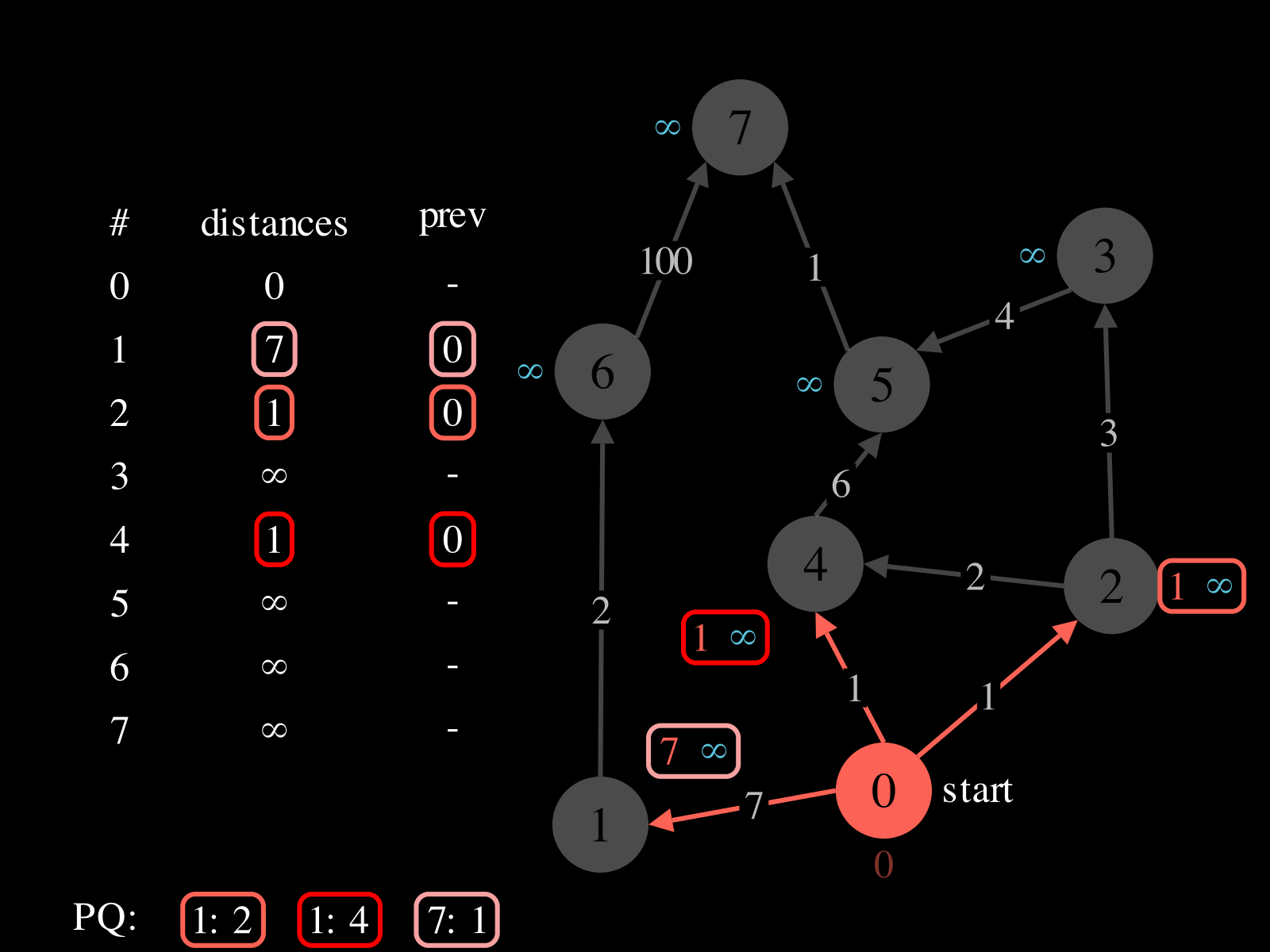
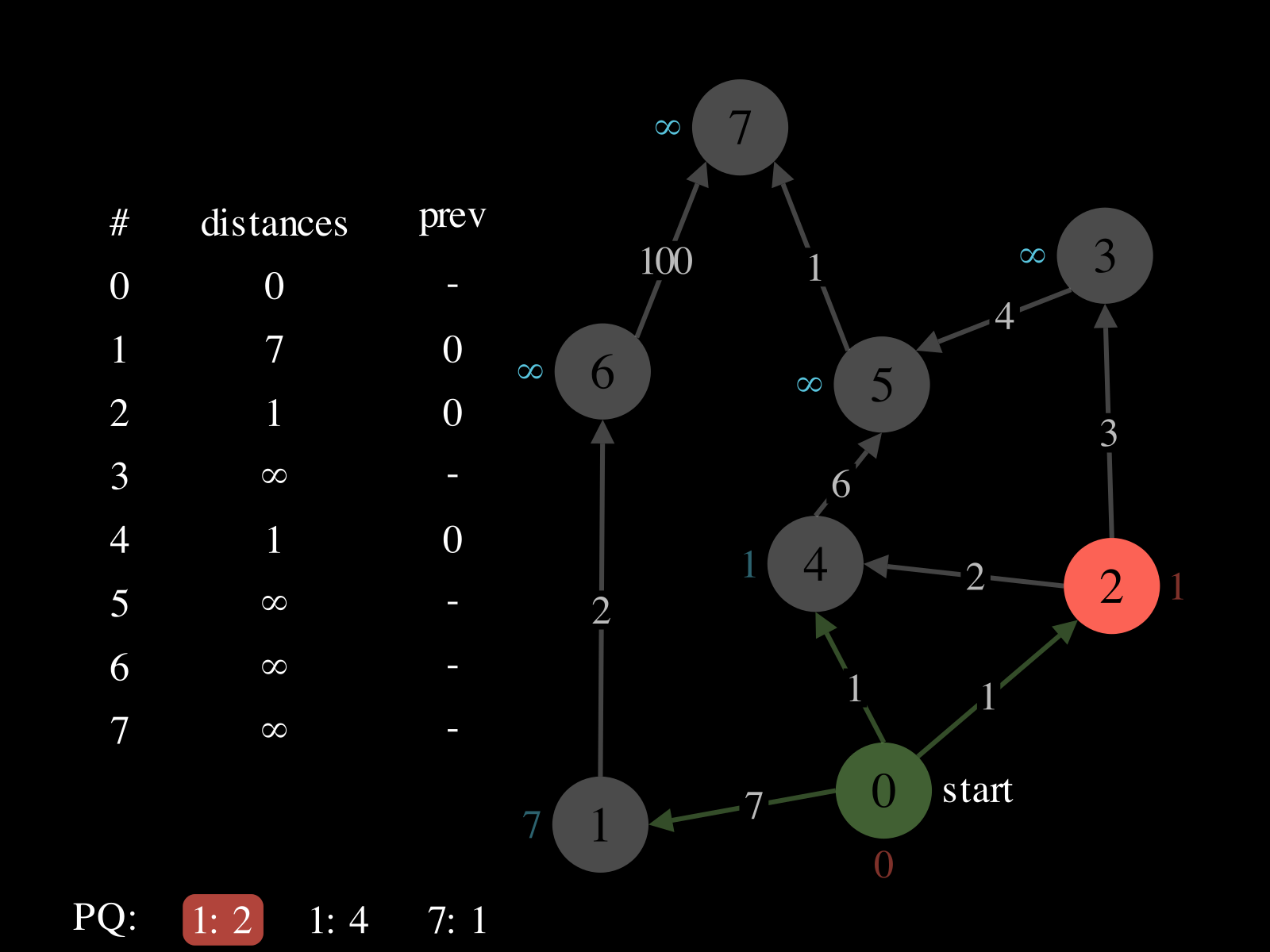
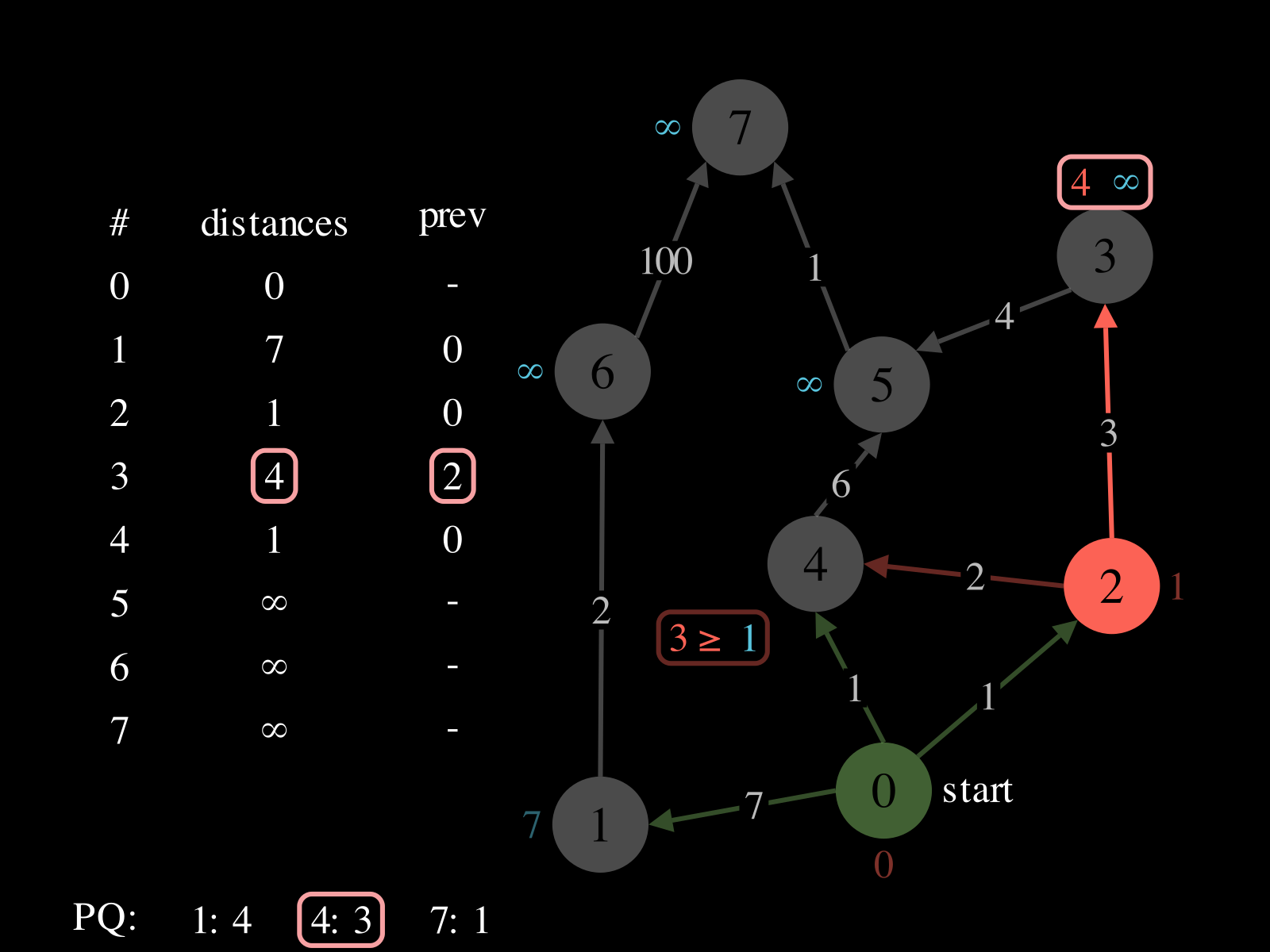
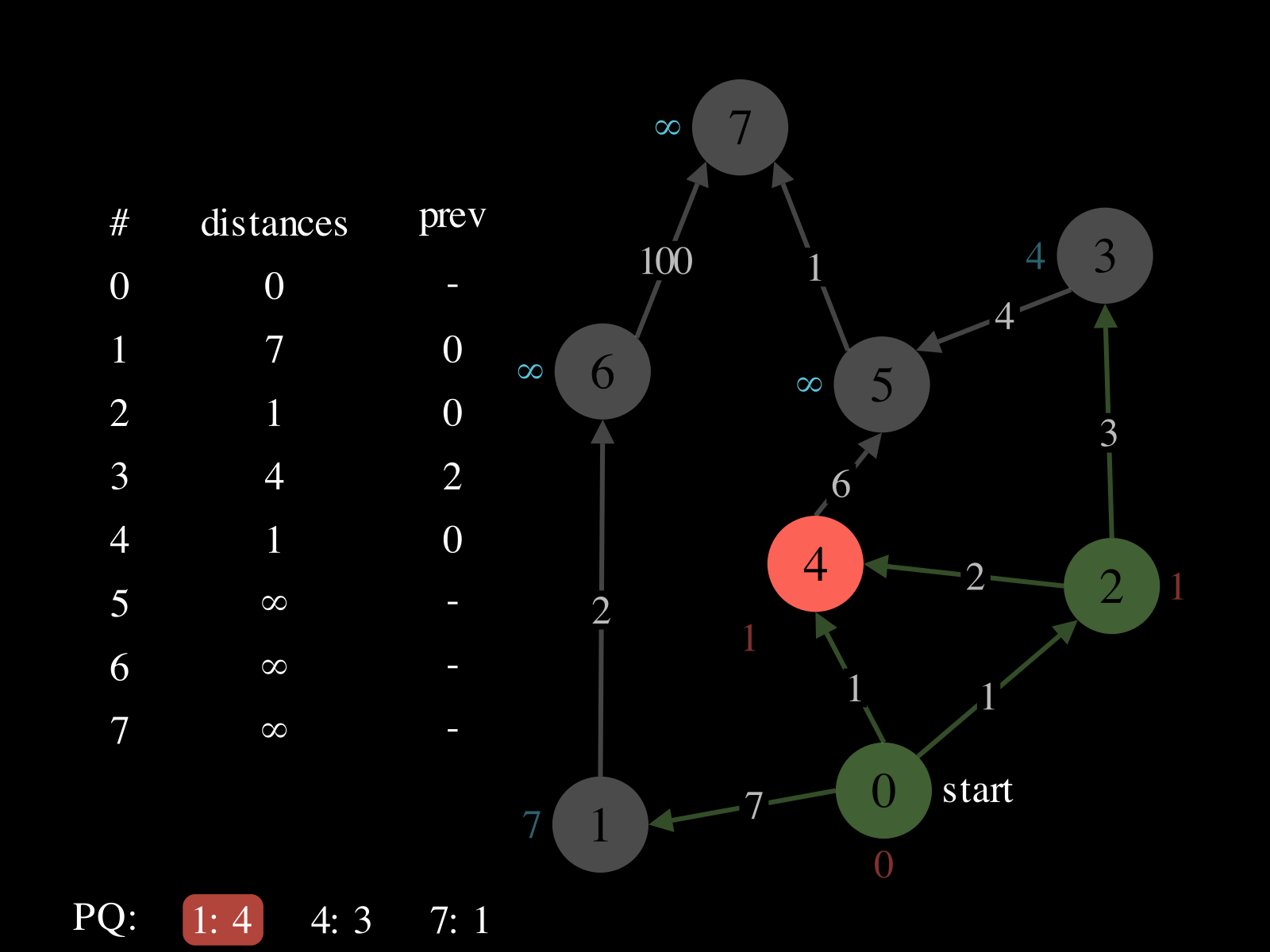
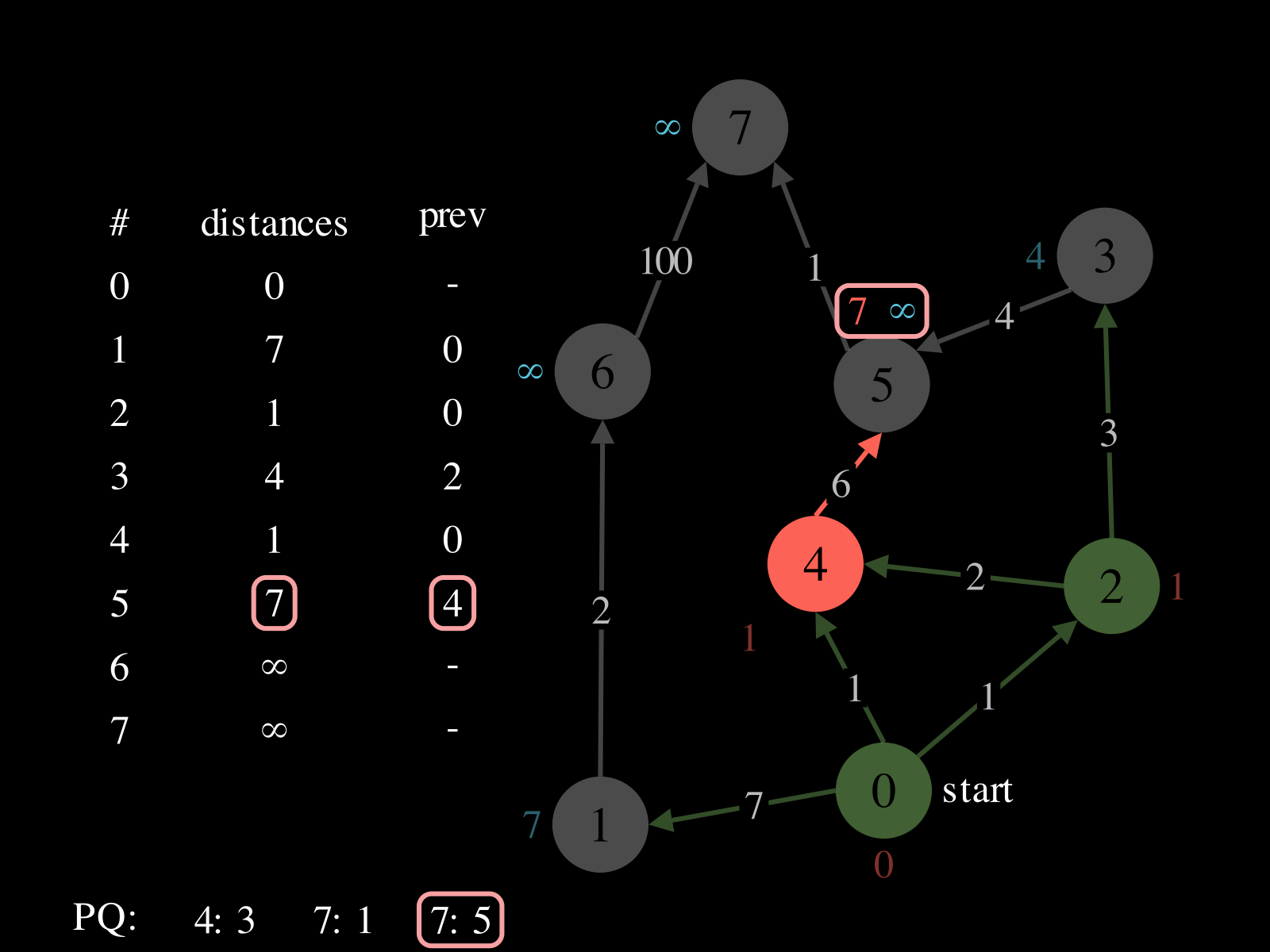
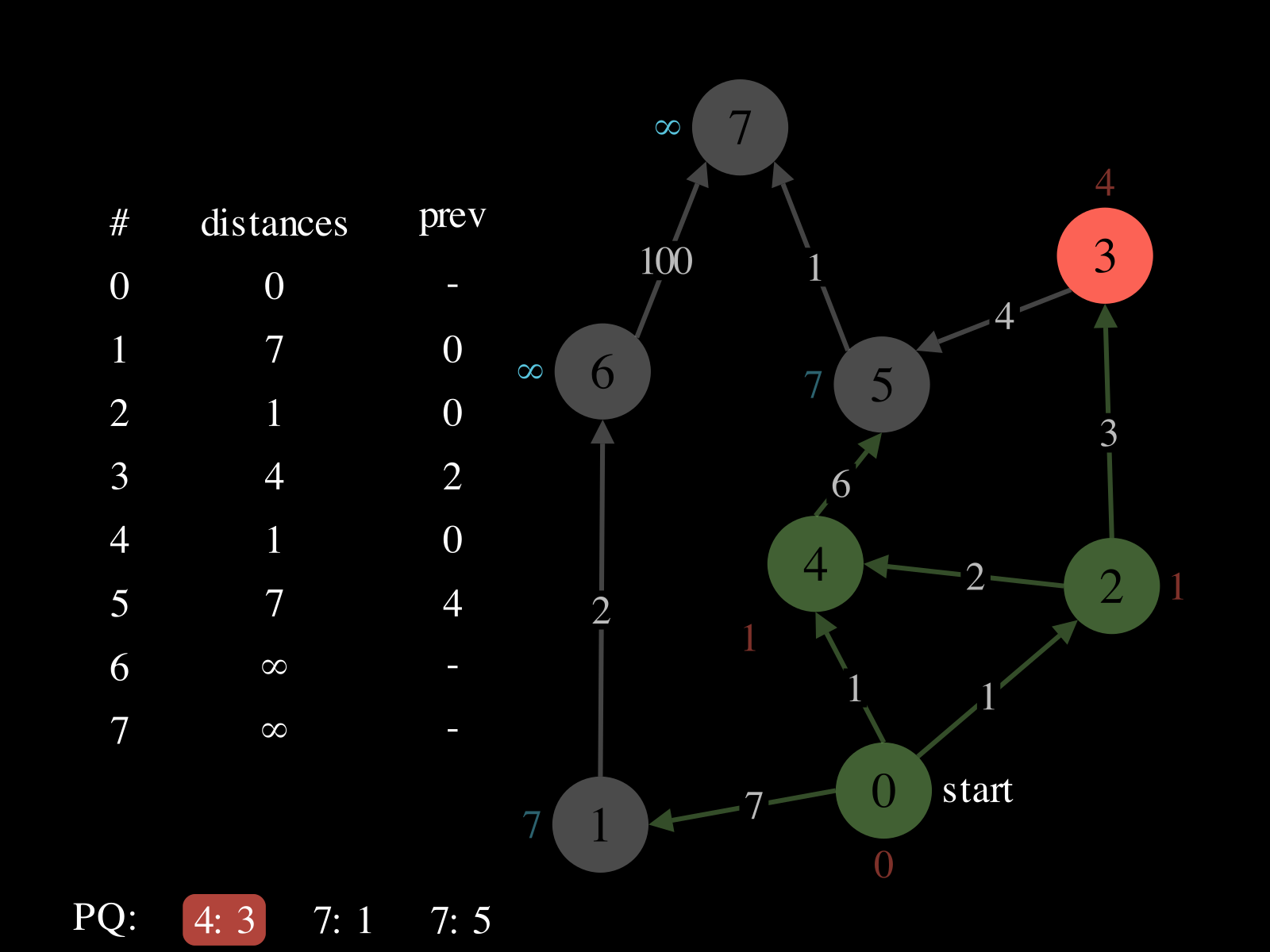
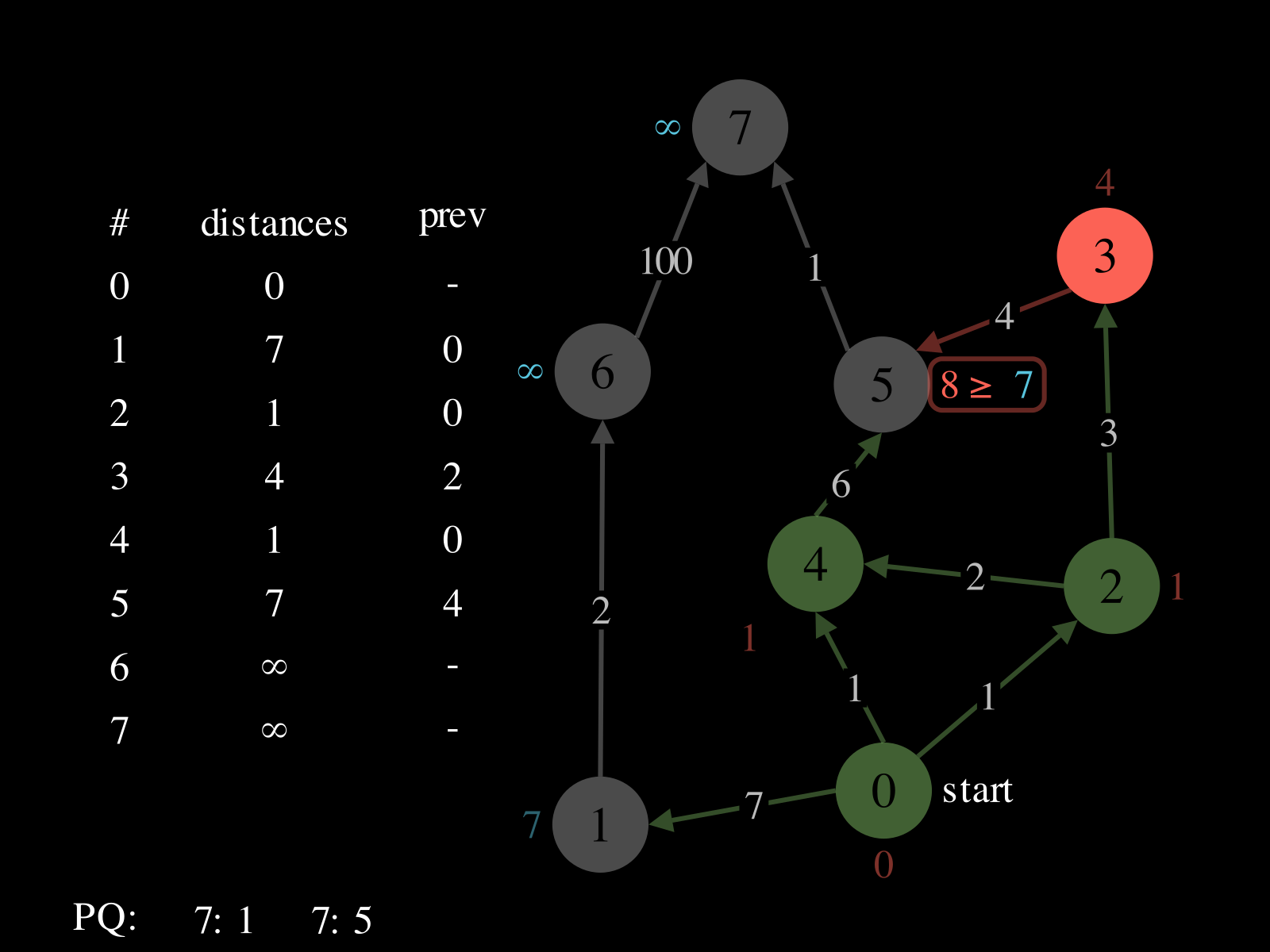
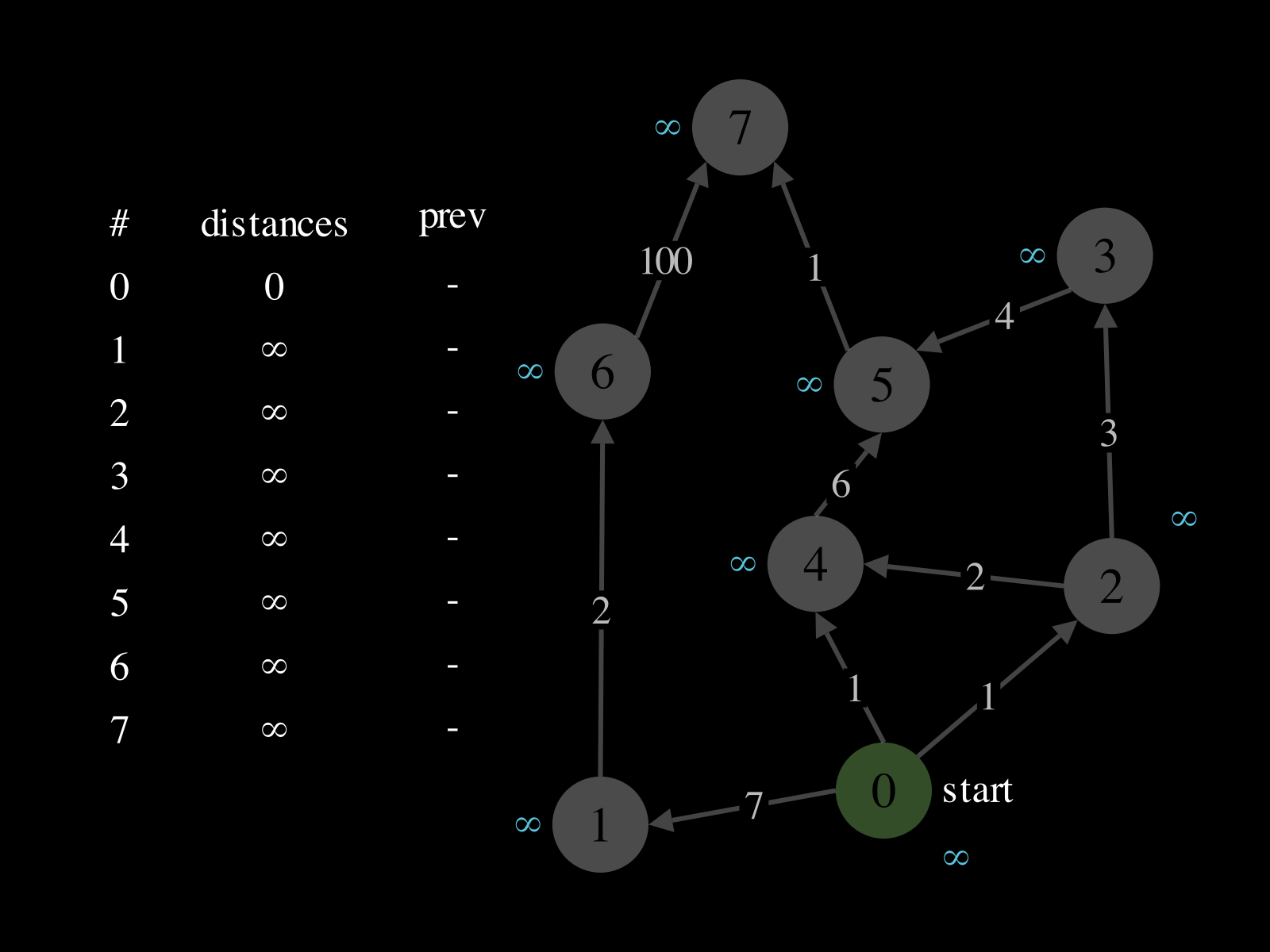
  • Initialize:
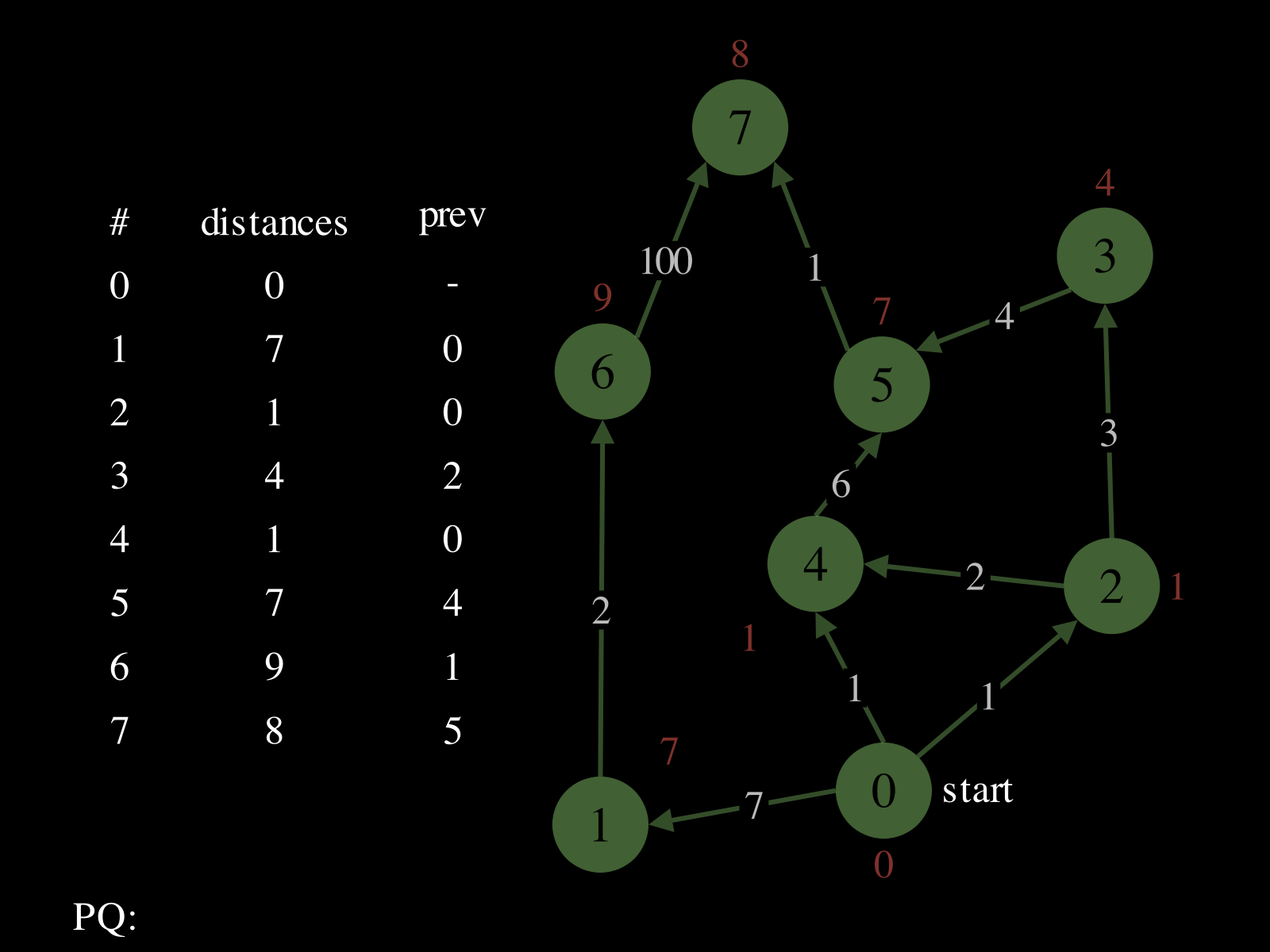
    • A priority queue PQ: where priorities are distances and values are vertices
    • A map distances: vertex → best distance so far
    • A map prev: vertex → previous vertex in best path found so far
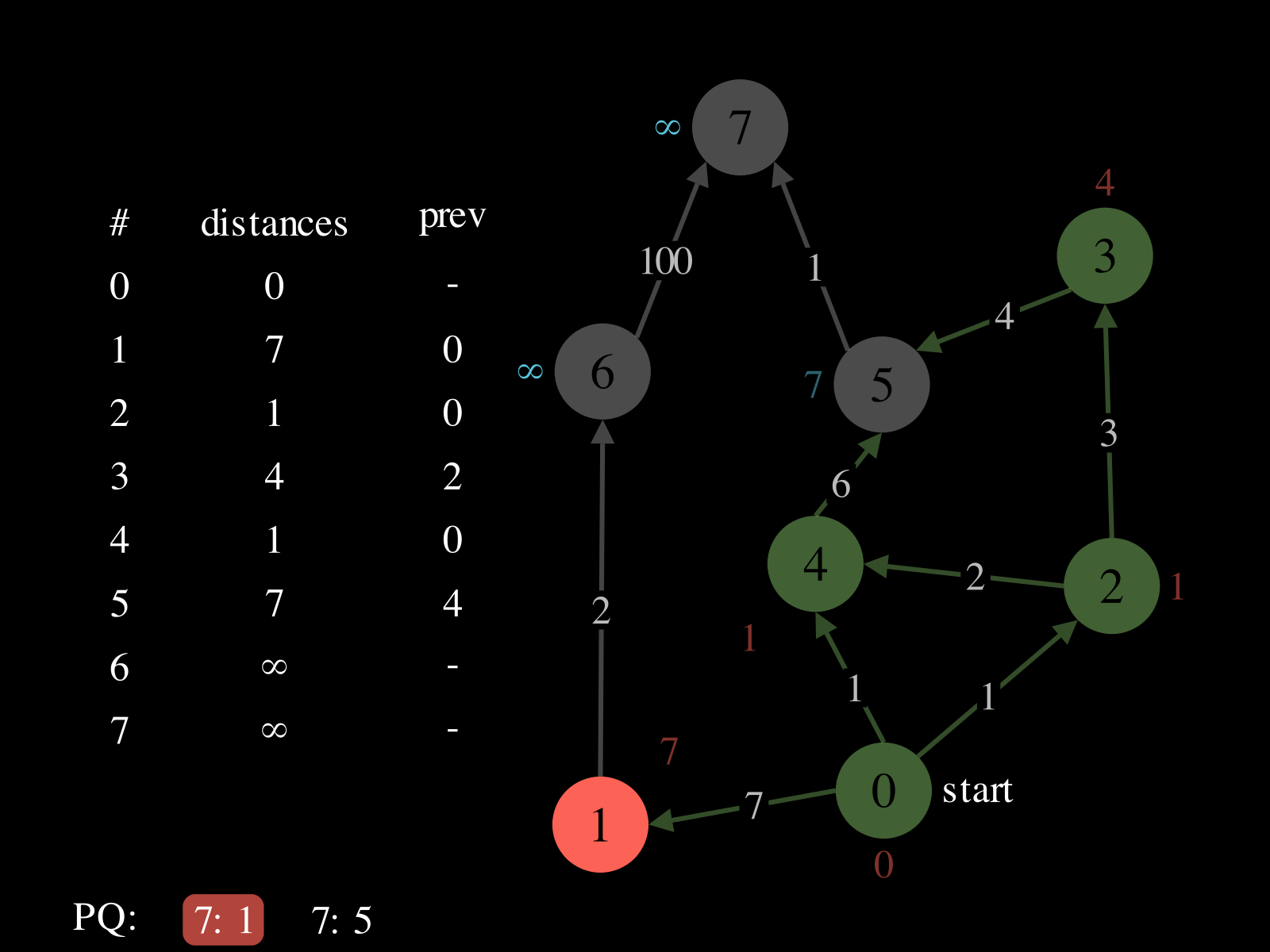
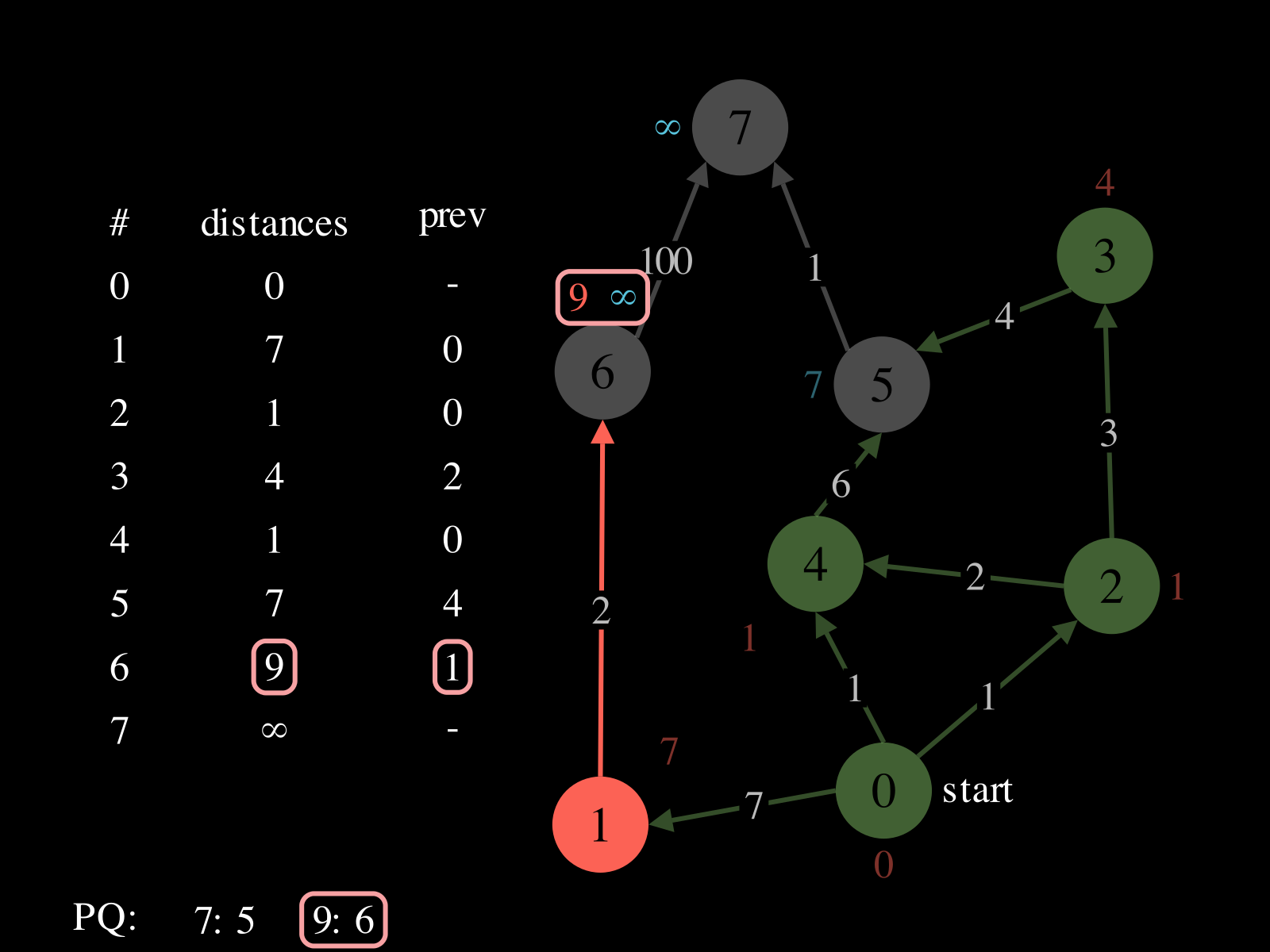
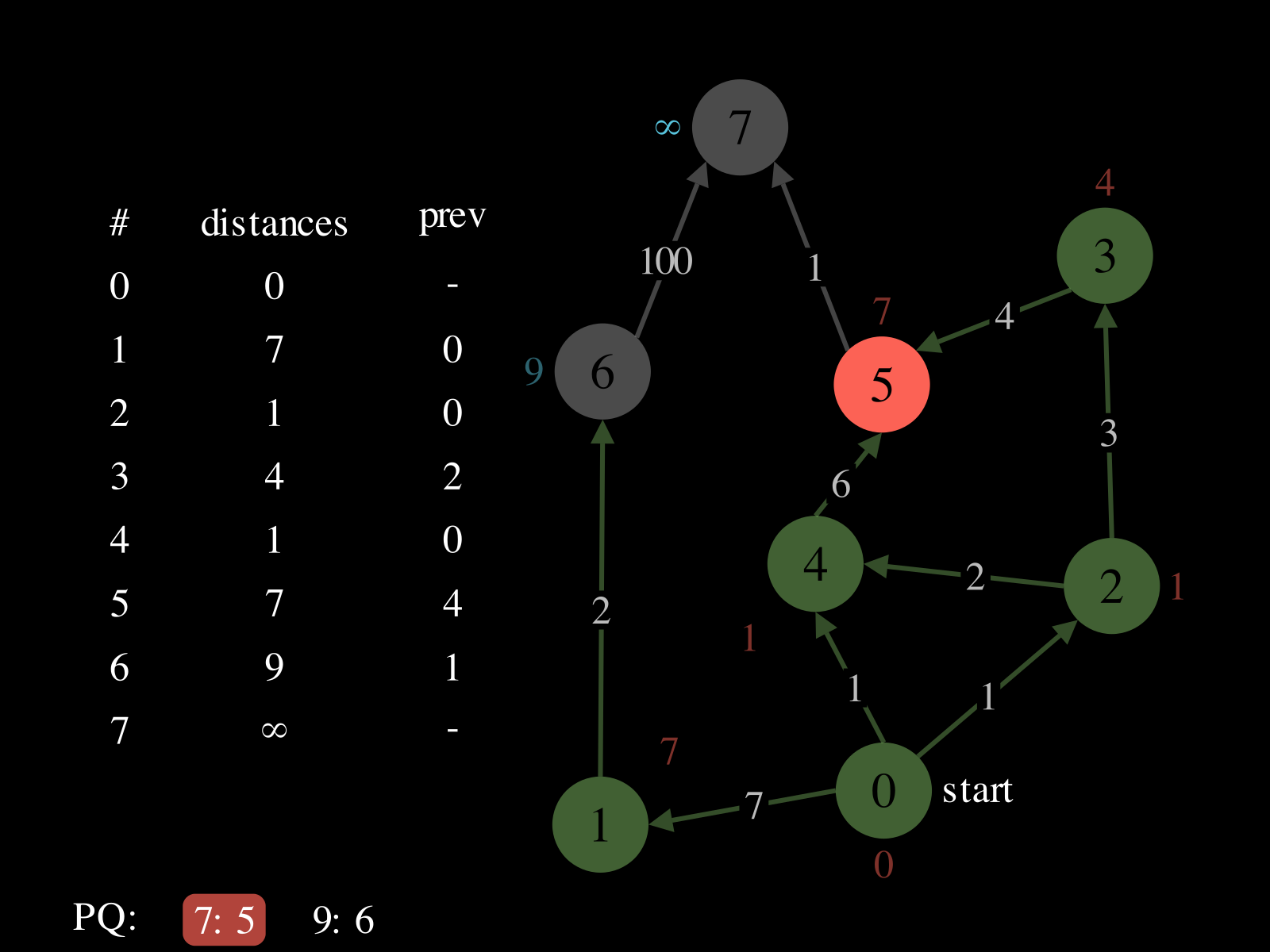
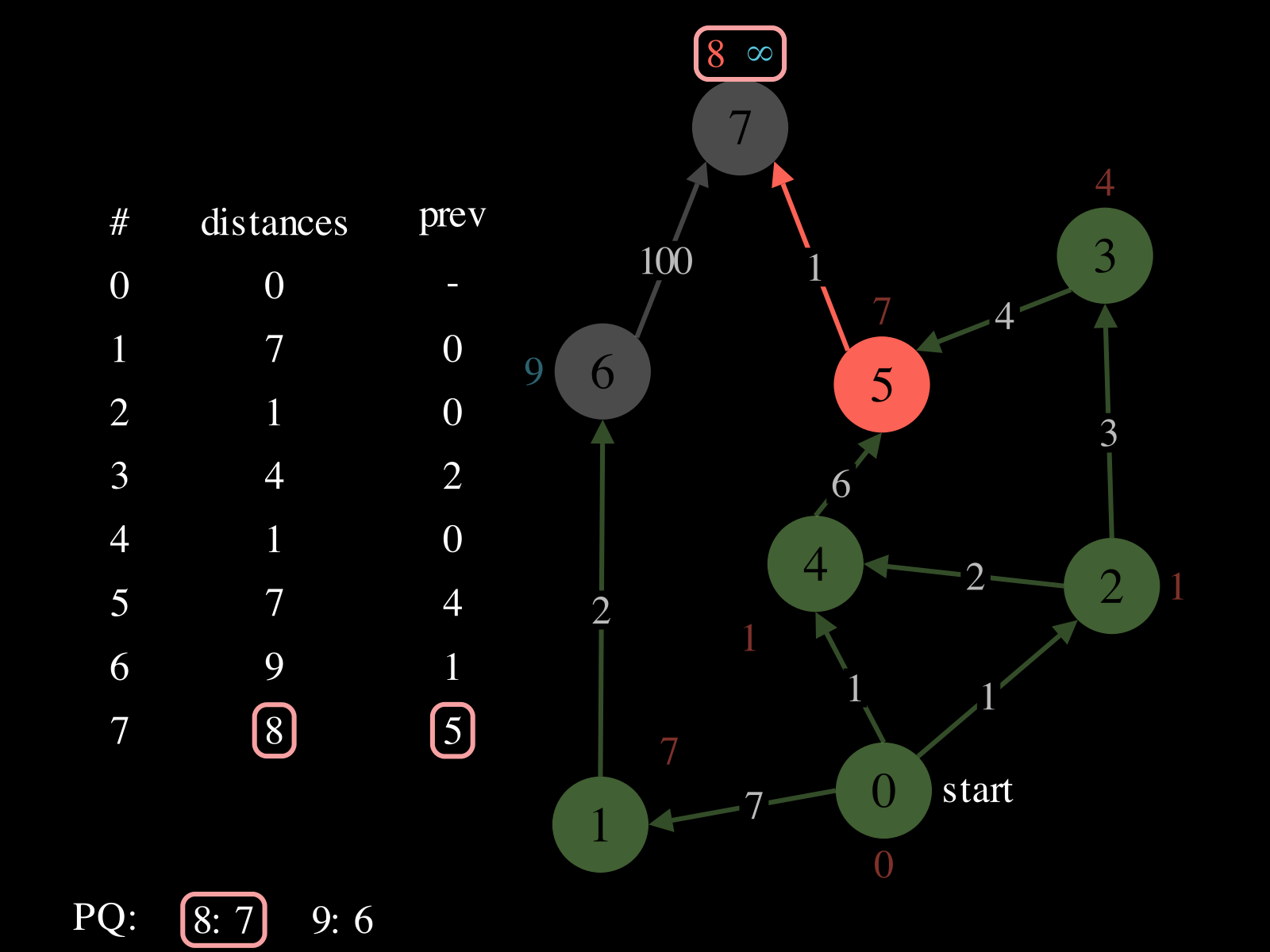
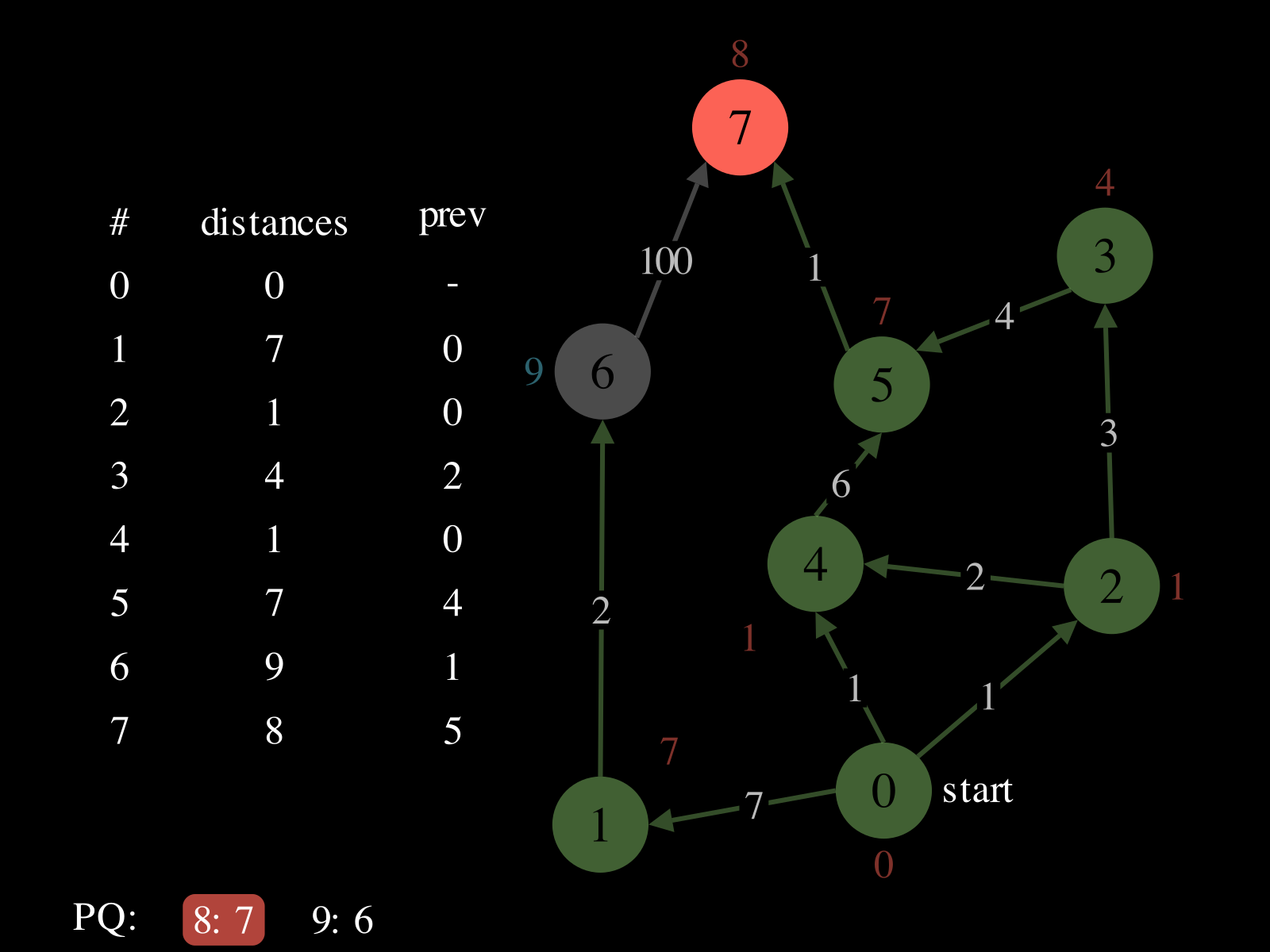
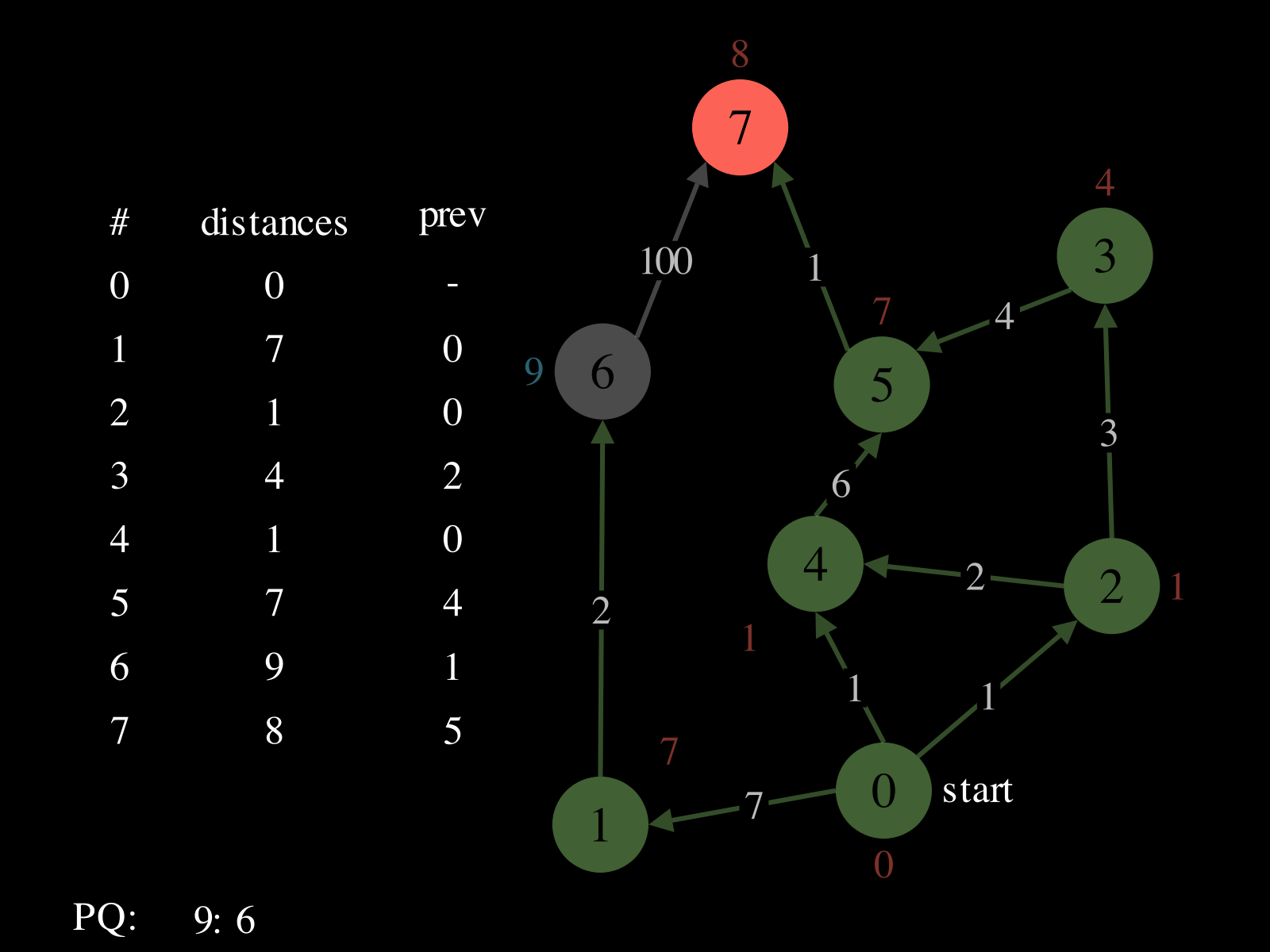
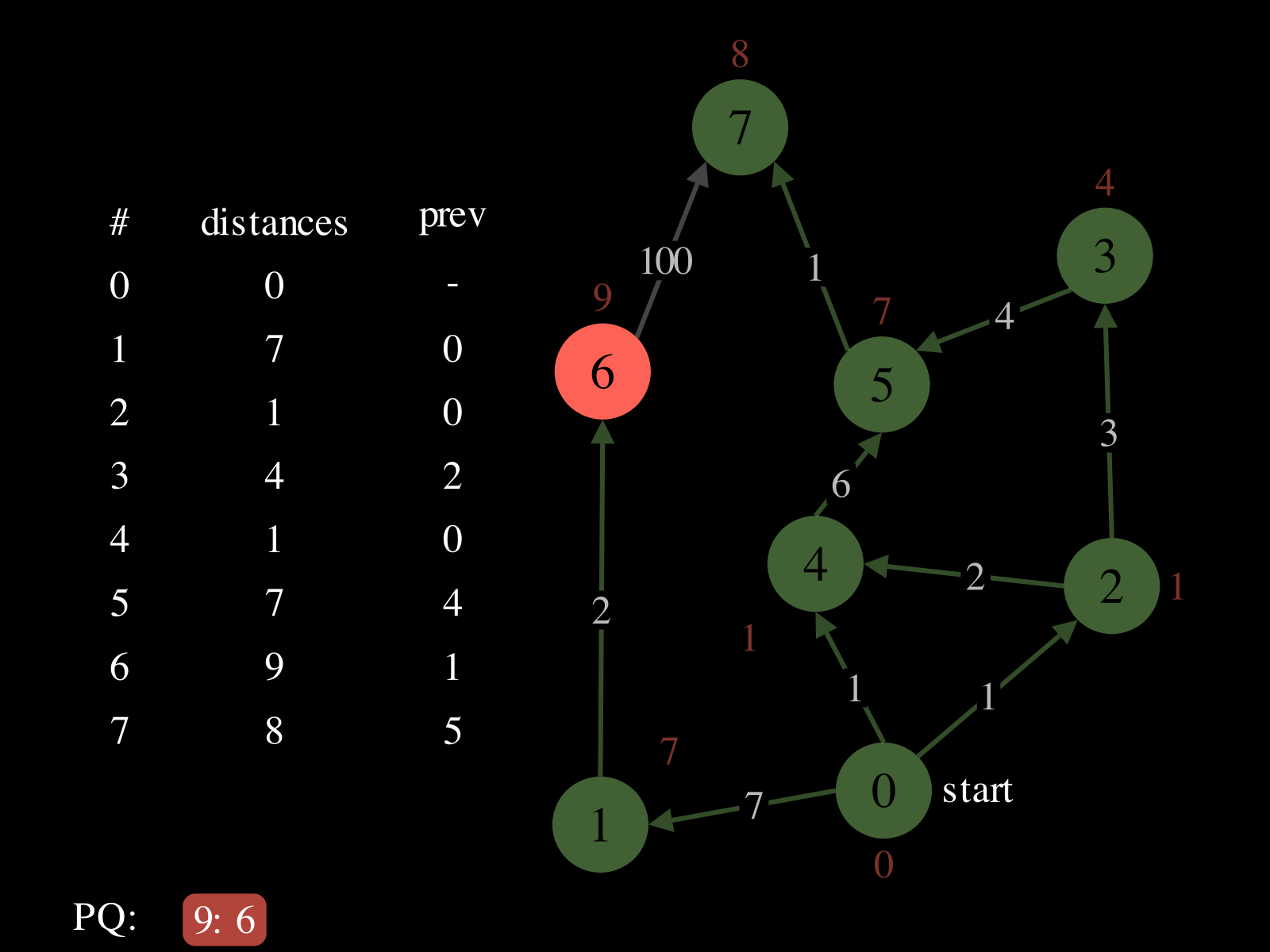
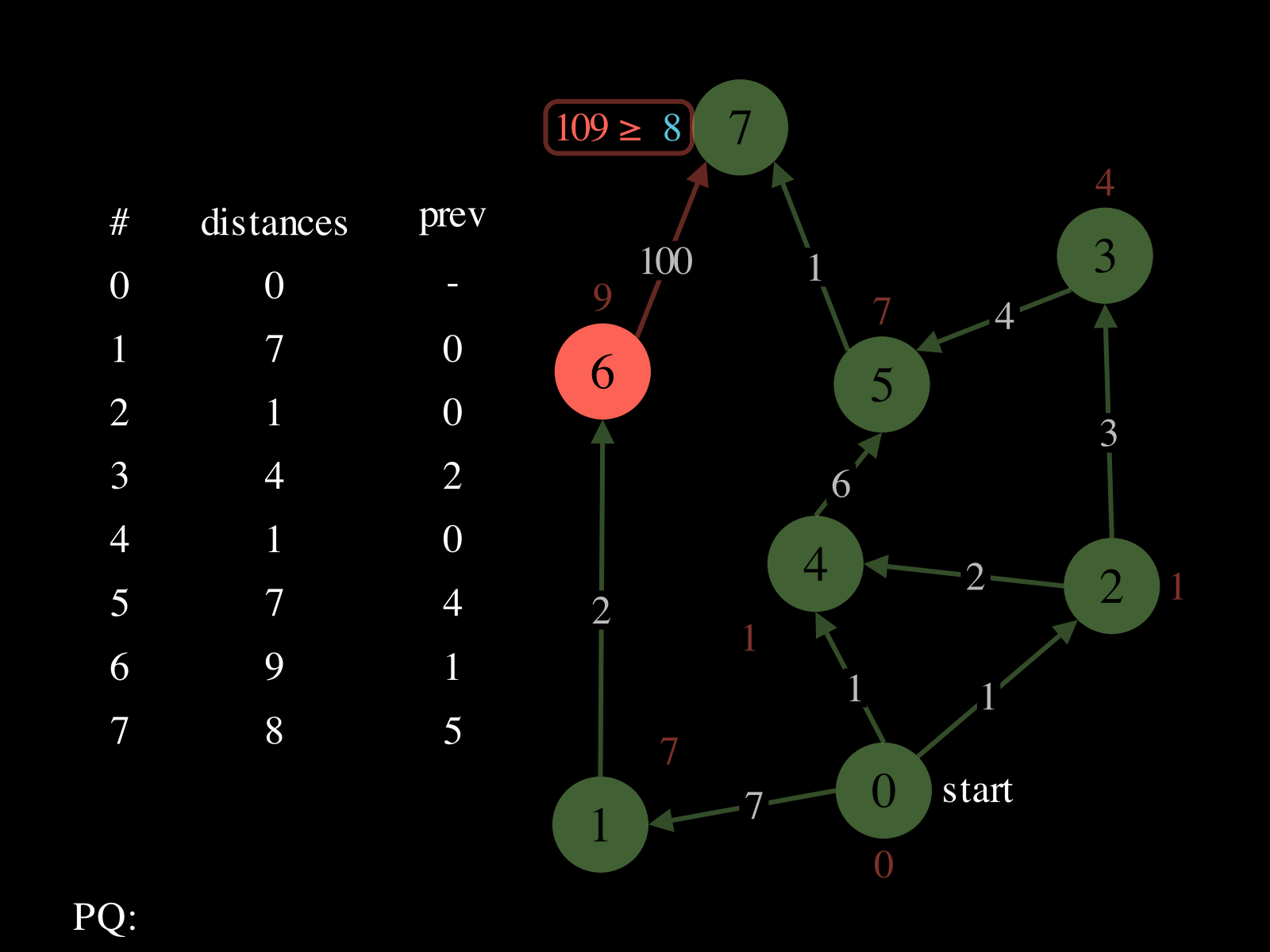
  • Repeat until PQ is empty:
    • Pop vertex v from PQ
    • Relax the outgoing edges of v by updating distances, PQ, and prev. See the picture above to see a relaxation step.

Behavior Slideshow

Slide 0 of 17
Slide 0
Slide 1
Slide 2
Slide 3
Slide 4
Slide 5
Slide 6
Slide 7
Slide 8
Slide 9
Slide 10
Slide 11
Slide 12
Slide 13
Slide 14
Slide 15
Slide 16
Slide 17
Use Arrow keys

Python Code

import heapq
# graph is a map from vertex v => list of outgoing edges
def dijkstra(graph, start):
    # dist is a map from vertex v => best distance found so far
    dist = {v: float("inf") for v in graph}
    dist[start] = 0
    pq = [(0, start)]
    prev = {}

    while pq:
        d, u = heapq.heappop(pq)
        for neighbor, weight in graph[u]:
            alt = d + weight
            if alt < dist[neighbor]:
                dist[neighbor] = alt
                prev[neighbor] = u
                heapq.heappush(pq, (alt, neighbor))
    return dist, prev

g = {
    0: [(1, 2), (2, 1)],
    1: [(2, 5), (3, 11), (4, 3)],
    2: [(5, 15)],
    3: [(4, 2)],
    4: [(2, 1), (5, 4), (6, 5)],
    5: [],
    6: [(3, 1), (5, 1)],
}
start = 0
dist, prev = dijkstra(g, start)
print("distance to 6 should be 10 and is", dist[6])

Concepts and Proof

Coming soon! Maybe.

Credits

Strongly influenced by Josh Hug's Djikstra's explanation from CS 61B, where I first learned Dijkstra's